自动求导与梯度计算

计算图

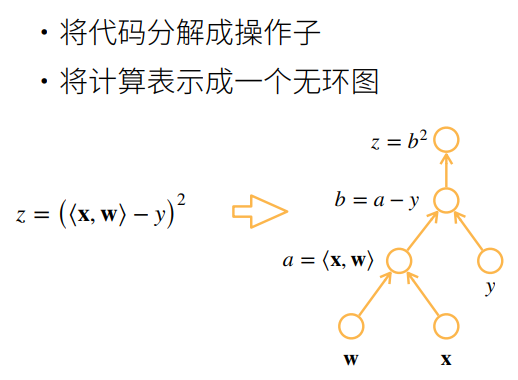
求导模型

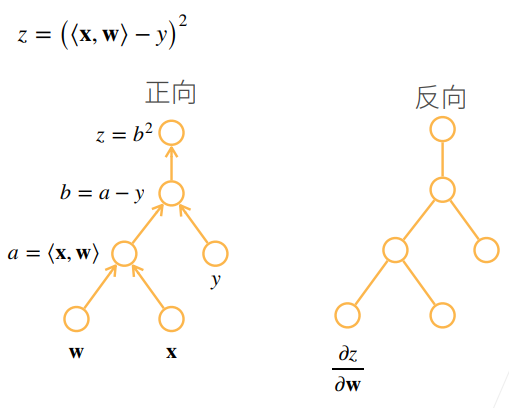
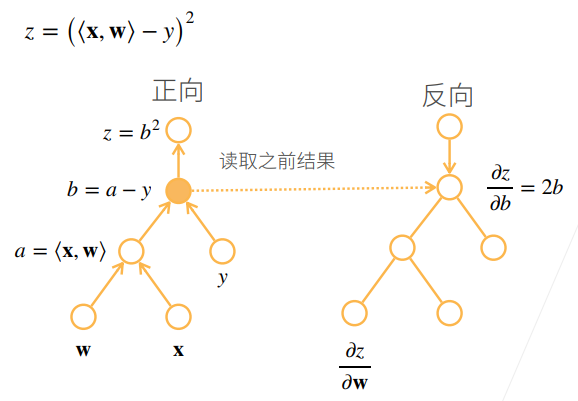
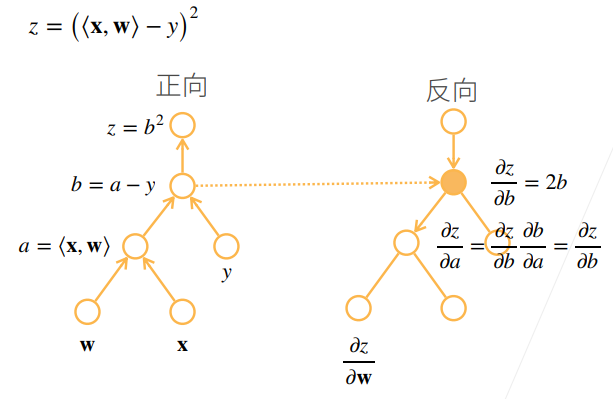
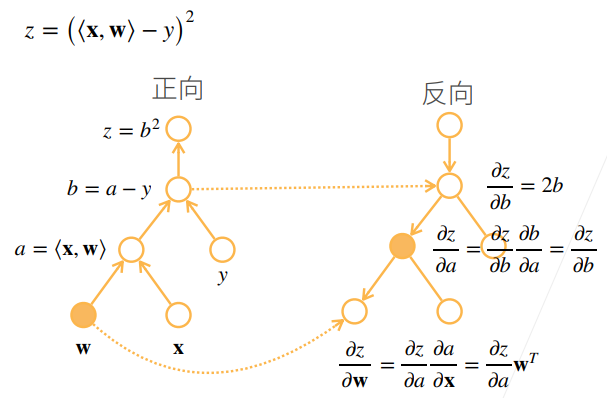
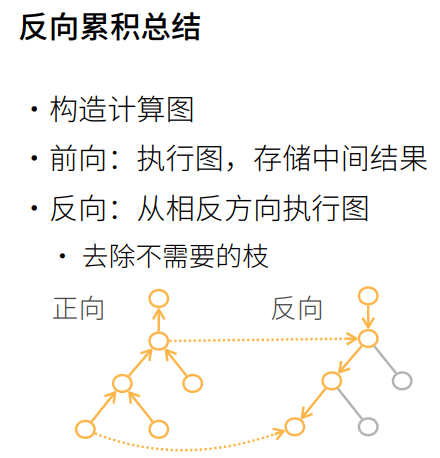
复杂度

代码实现

import torch

# 定义张量
x = torch.arange(4.0, requires_grad=True)  # requires_grad=True表示需要求导
print(x)
print(x.grad)  # x的梯度

# 表示函数
y = 2 * torch.dot(x, x)
print(y)

# 通过调用反向传播函数来自动计算y关于x每个分量的梯度
y.backward()  # 反向传播
print(x.grad)  # x的梯度
print(x.grad == 4 * x)  # 验证梯度是否正确

输出结果：

tensor([0., 1., 2., 3.], requires_grad=True)
None
tensor(28., grad_fn=<MulBackward0>)
tensor([ 0.,  4.,  8., 12.])
tensor([True, True, True, True])

如果要重新调用反向传播函数，则需要将之前的梯度清零：

x.grad.zero_()  # 清零梯度
y.backward()  # 再次反向传播
print(x.grad)  # x的梯度