Bagging
Bagging 集成原理
假如,我们要把下面的圈和方块进行分类:
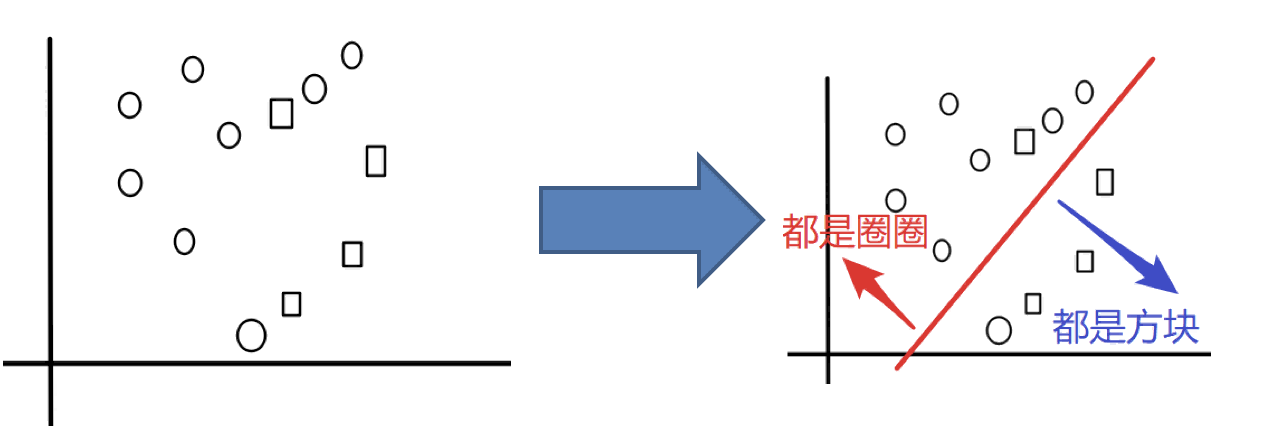
Bagging 集成方法的基本思路是:
1.采样不同数据集
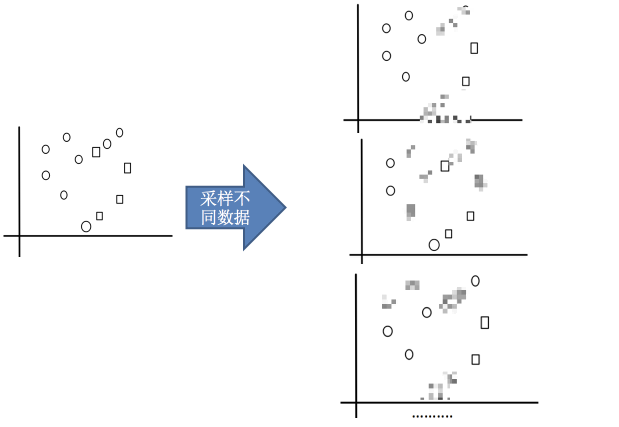
2.训练分类器
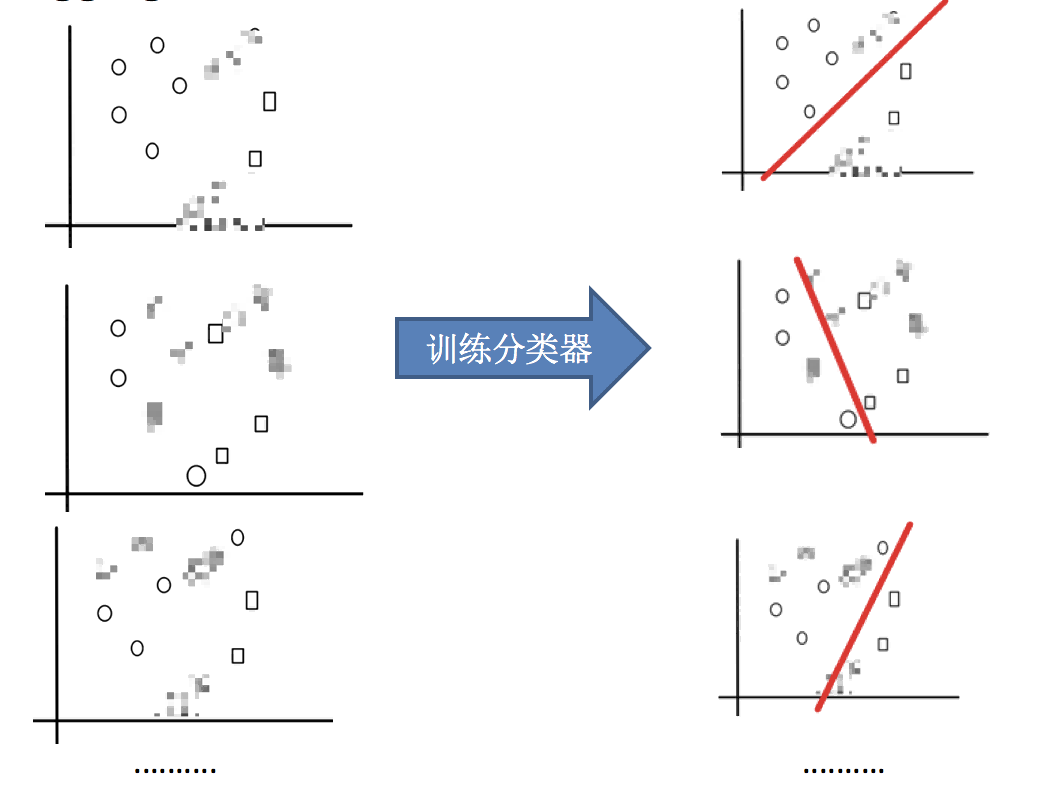
3.平权投票,获取最终结果
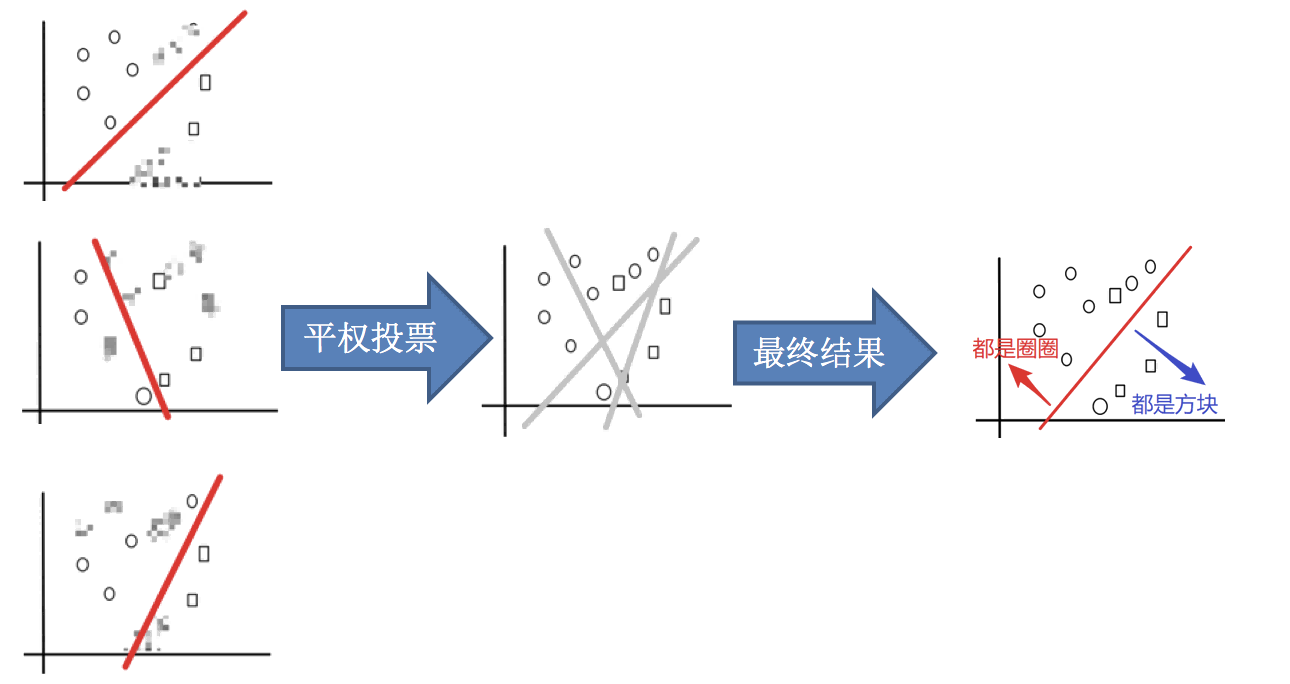
合起来看就是:
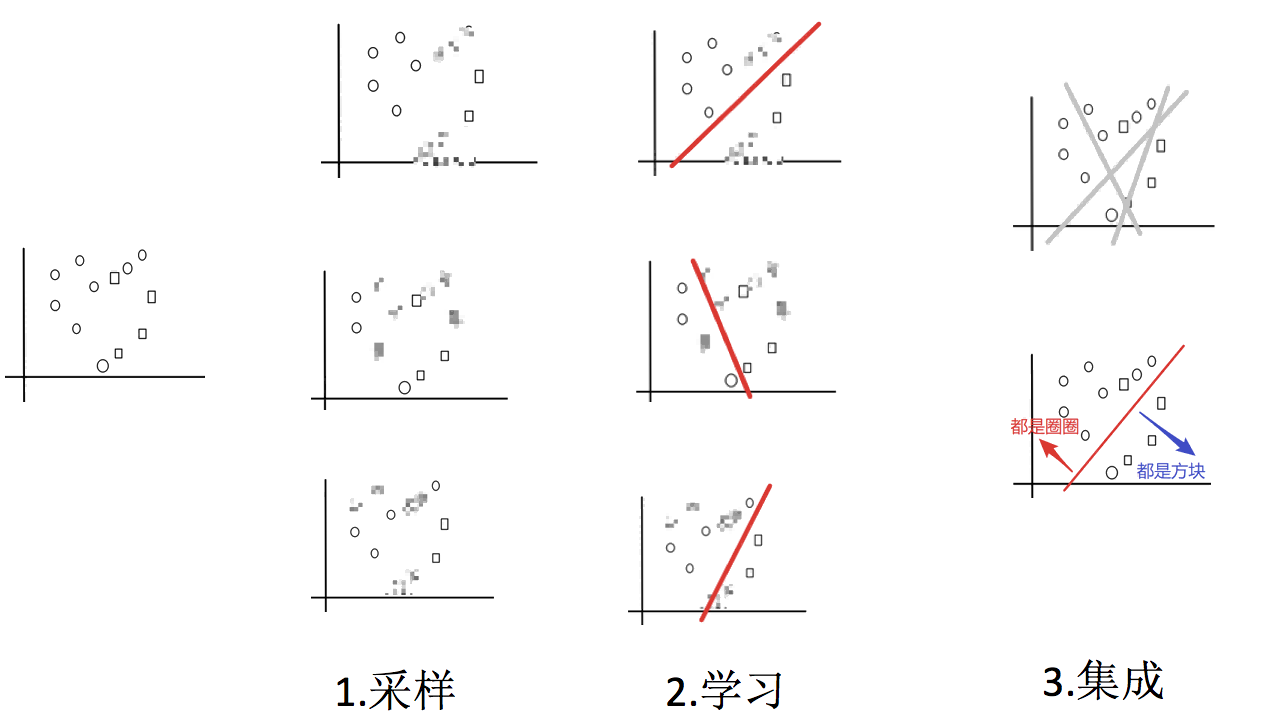
这就是 Bagging 集成方法的基本思路。
随机森林
在机器学习中,随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。
随机森林 = Bagging + 决策树
例如, 如果你训练了 5 个树, 其中有 4 个树的结果是 True, 1 个树的结果是 False, 那么最终投票结果就是 True
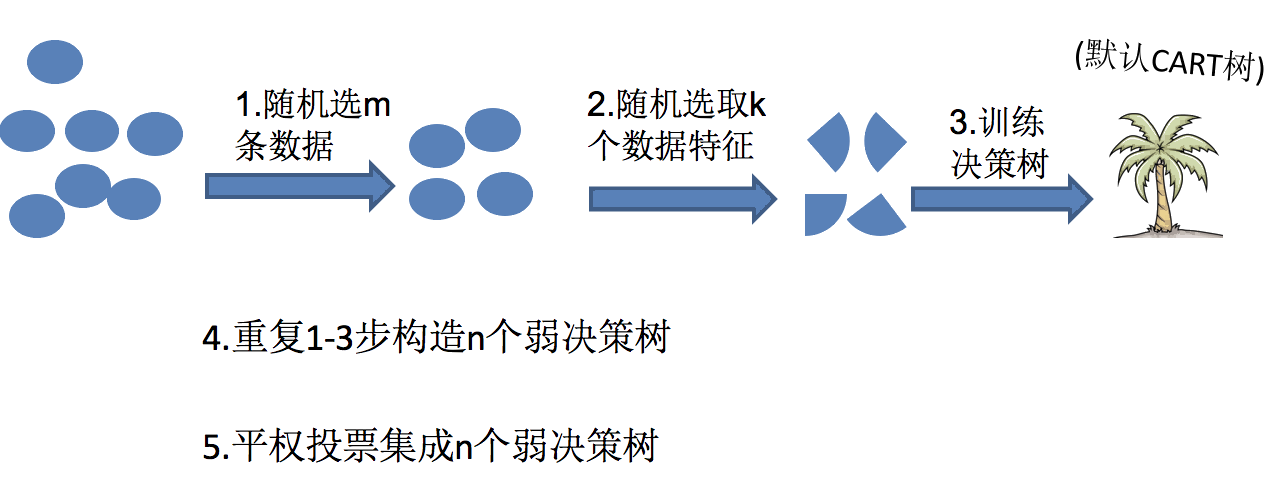
随机森林够造过程中的关键步骤(M 表示特征数目):
- 一次随机选出一个样本,有放回的抽样,重复 N 次(有可能出现重复的样本)
- 随机选出 m 个特征, m << M,建立决策树
为什么要随机抽样训练集?
如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的
为什么要有放回地抽样?
如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是“有偏的”,都是绝对“片面的”(当然这样说可能不对),也就是说每棵树训练出来都是有很大的差异的;而随机森林最后分类取决于多棵树(弱分类器)的投票表决。
优点
Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging 集成学习方法
经过上面方式组成的集成学习方法:
- 均可在原有算法上提高约 2% 左右的泛化正确率
- 简单, 方便, 通用
