支持向量机(SVM)
支持向量机(support vector machines,SVM)是一种二分类模型,它将实例的特征向量映射为空间中的一些点,SVM 的目的就是想要画出一条线,以 “最好地” 区分这两类点,以至如果以后有了新的点,这条线也能做出很好的分类。SVM 适合中小型数据样本、非线性、高维的分类问题。
SVM 最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在 1963 年提出,目前的版本(soft margin)是由 Corinna Cortes 和 Vapnik 在 1993 年提出,并在 1995 年发表。深度学习(2012)出现之前,SVM 被认为机器学习中近十几年来最成功,表现最好的算法。
与我们之前提到的降维相反,SVM 通过“升维”的方式进行建模。
SVM 是一种有监督学习、二分类的算法。
SVM 基本概念
将实例的特征向量(以二维为例)映射为空间中的一些点,如下图的实心点和空心点,它们属于不同的两类。SVM 的目的就是想要画出一条线,以“最好地”区分这两类点,以至如果以后有了新的点,这条线也能做出很好的分类。
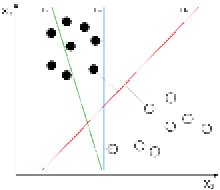
我们通过一些问题来对所有的细节进行拆解:
Q1:能够画出多少条线对样本点进行区分?
答:线是有无数条可以画的,区别就在于效果好不好,每条线都可以叫做一个划分超平面。比如上面的绿线就不好,蓝线还凑合,红线看起来就比较好。我们所希望找到的这条效果最好的线就是具有 “最大间隔的划分超平面”。
Q2:为什么要叫作“超平面”呢?
答:因为样本的特征很可能是高维的,此时样本空间的划分就不是一条线了。
Q3:画线的标准是什么?/ 什么才叫这条线的效果好?/ 哪里好?
答:SVM 将会寻找可以区分两个类别并且能使间隔(margin)最大的划分超平面。比较好的划分超平面,样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。
Q4:间隔(margin)是什么?
答:对于任意一个超平面,其两侧数据点都距离它有一个最小距离(垂直距离),这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin,虚线是由距离中央实线最近的两个点所确定出来的(也就是由支持向量决定)。但此时 margin 比较小,如果用第二种方式画,margin 明显变大也更接近我们的目标。
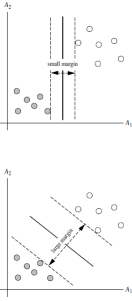
Q5:为什么要让 margin 尽量大? 答:因为大 margin 犯错的几率比较小,也就是更鲁棒啦。
Q6:支持向量是什么? 答:从上图可以看出,虚线上的点到划分超平面的距离都是一样的,实际上只有这几个点共同确定了超平面的位置,因此被称作 “支持向量(support vectors)”,“支持向量机” 也是由此来的。
hard-margin SVM
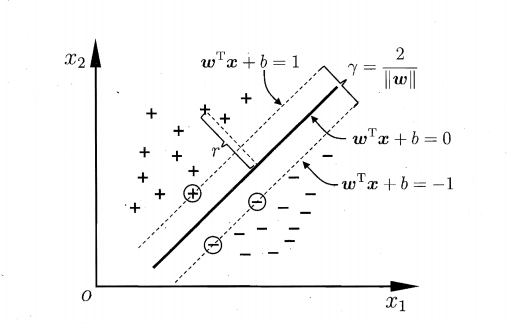
划分超平面可以定义为一个线性方程:
只要确定了法向量 w 和位移 b ,就可以唯一地确定一个划分超平面。
利用 Karush-Kuhn-Tucker (KKT)条件和拉格朗日公式,可以推出 MMH 可以被表示为以下“决定边界 (decision boundary)”
此方程就代表了边际最大化的划分超平面。
每当有新的测试样本 X ,将它带入该方程,看看该方程的值是正还是负,根据符号进行归类。
SVM 扩展到多分类问题
SVM 扩展可解决多个类别分类问题:
- 对于每个类,有一个当前类和其他类的二类分类器(one-vs-rest)
- 将多分类问题转化为 n 个二分类问题,n 就是类别个数。
SVM 算法特性
- 训练好的模型的算法复杂度是由支持向量的个数决定的,而不是由数据的维度决定的。所以 SVM 不太容易产生 overfitting。
- SVM 训练出来的模型完全依赖于支持向量,即使训练集里面所有非支持向量的点都被去除,重复训练过程,结果仍然会得到完全一样的模型。
- 一个 SVM 如果训练得出的支持向量个数比较少,那么 SVM 训练出的模型比较容易被泛化。
