模型评估
对于聚类算法,有监督学习的评估方法大部分都不再适用了,我们需要一些新的评估方法。
误差平方和(SSE, The sum of squares due to error)
非常直白,例如下图:

在 k-means 中:
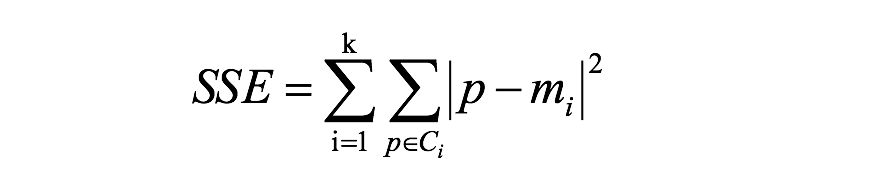
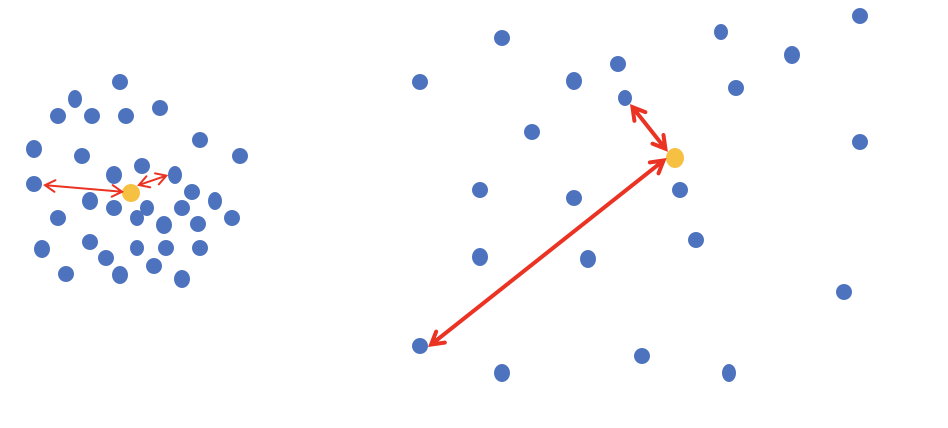
公式各部分内容:
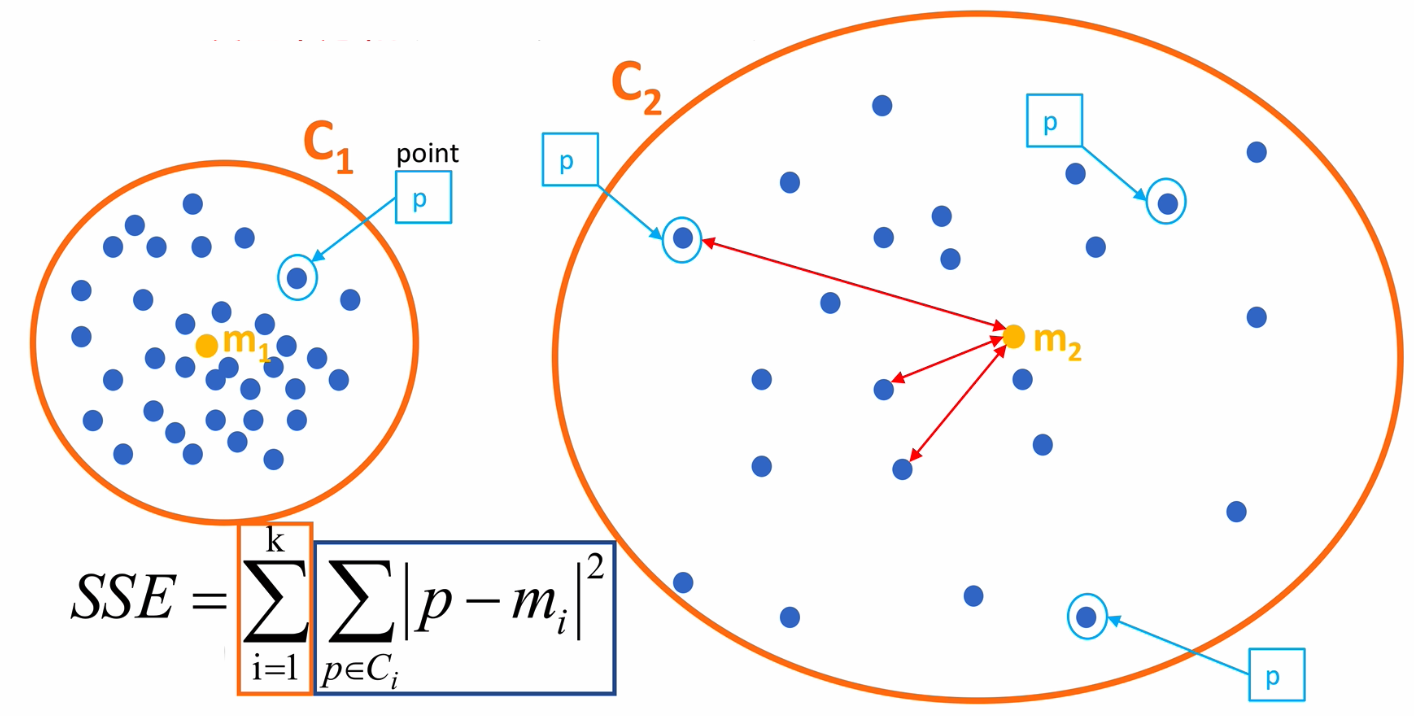
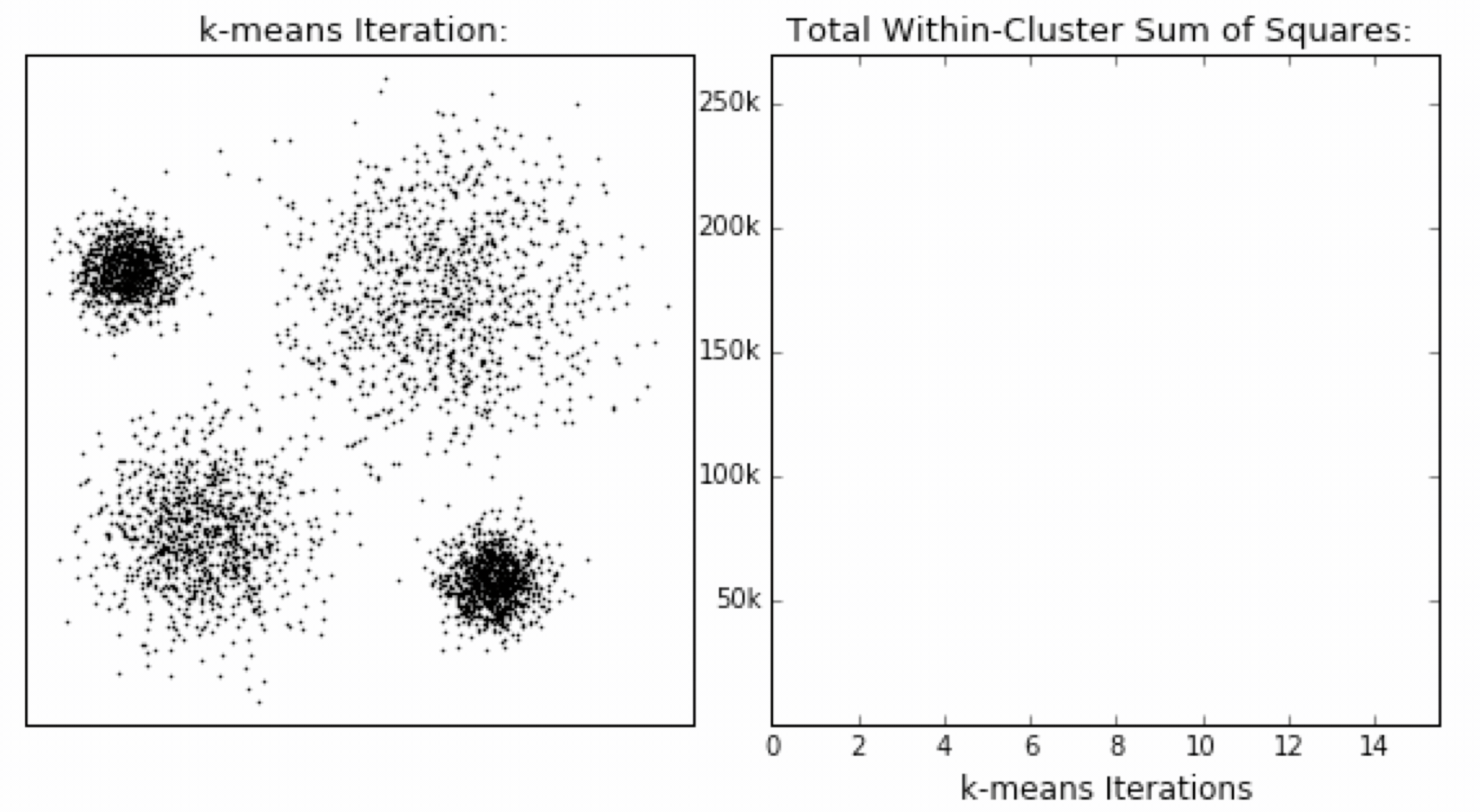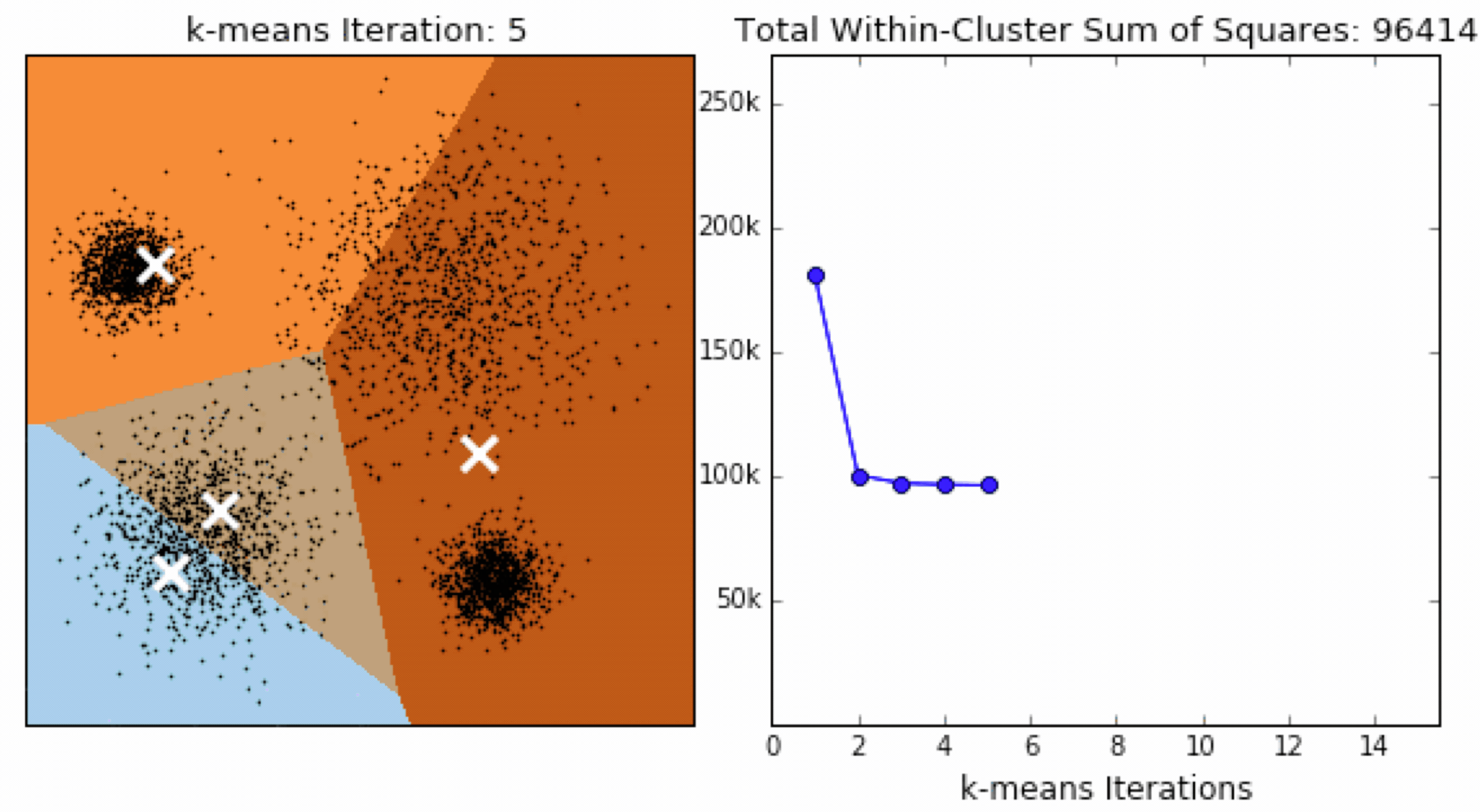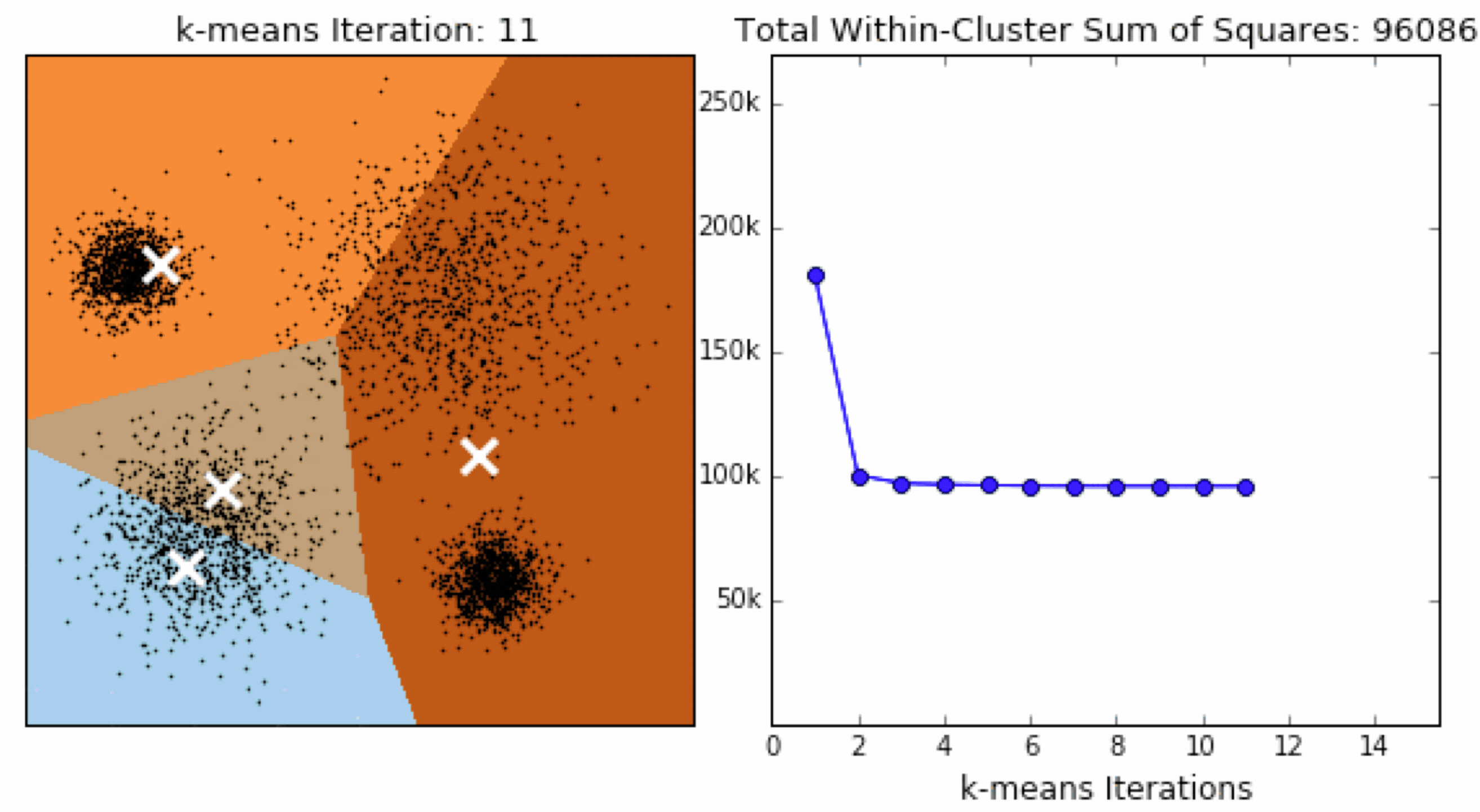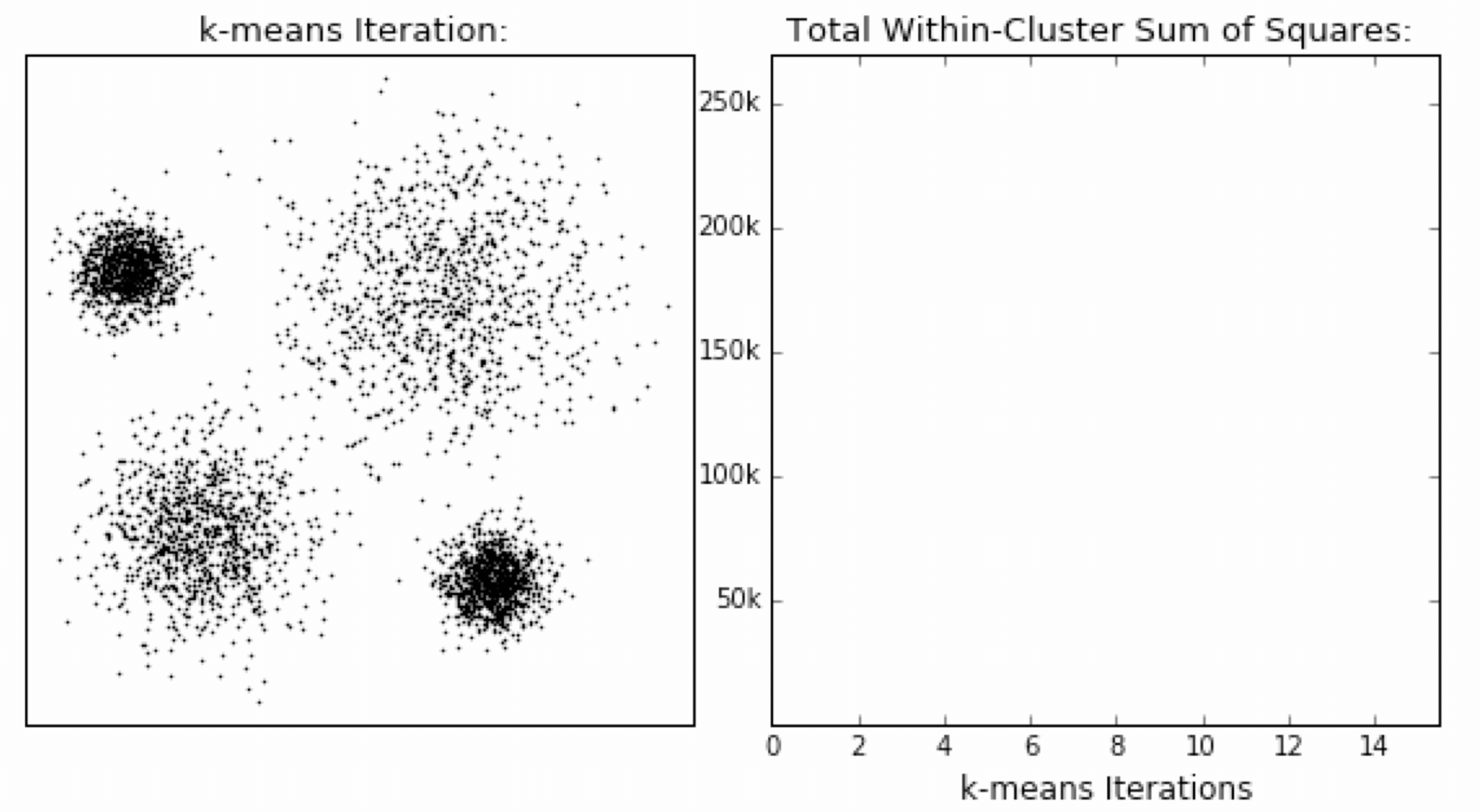
SSE 图最终的结果是对图松散度的衡量,随着聚类迭代其值会越来越小,直到最后趋于稳定:

如果质心的初始值选择不好,SSE 只会达到一个不怎么好的局部最优解:
“肘”方法 (Elbow method) — 确定 K 值
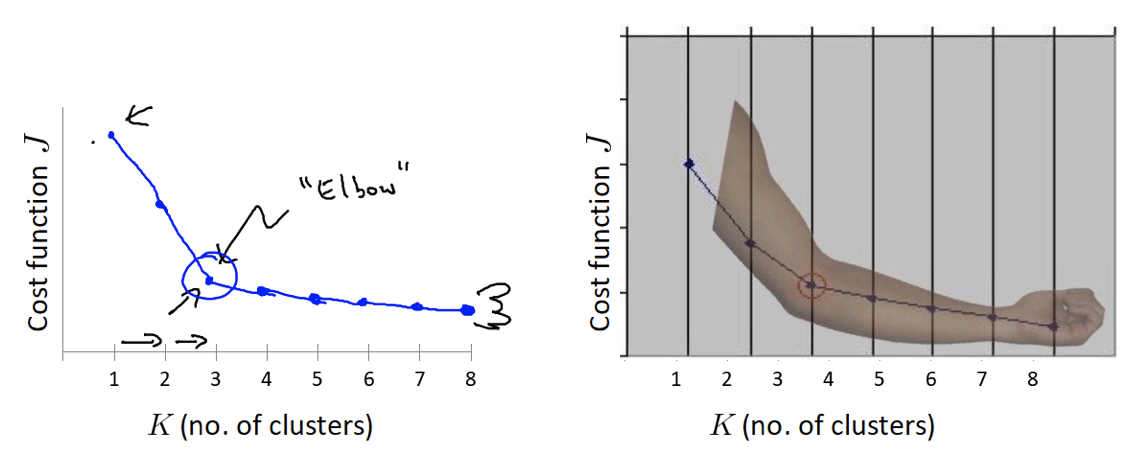
- 对于 n 个点的数据集,迭代计算 k from 1 to n,每次聚类完成后计算每个点到其所属的簇中心的距离的平方和;
- 平方和是会逐渐变小的,直到 k==n 时平方和为 0,因为每个点都是它所在的簇中心本身。
- 在这个平方和变化过程中,会出现一个拐点也即“肘”点,下降率突然变缓时即认为是最佳的 k 值。
在决定什么时候停止训练时,肘形判据同样有效,数据通常有更多的噪音,在增加分类无法带来更多回报时,我们停止增加类别。
[选读]轮廓系数法(Silhouette Coefficient)
结合了聚类的凝聚度(Cohesion)和分离度(Separation),用于评估聚类的效果:
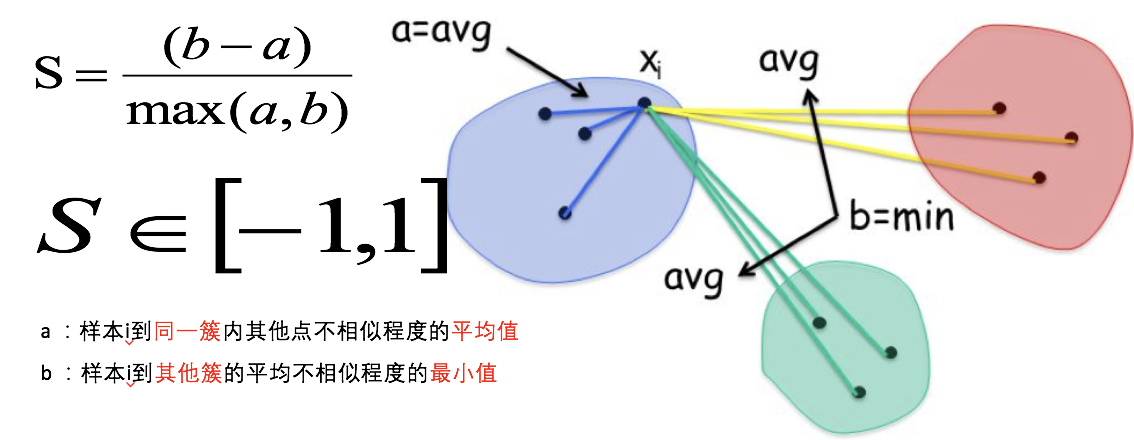
其目的在于使内部距离最小化,外部距离最大化
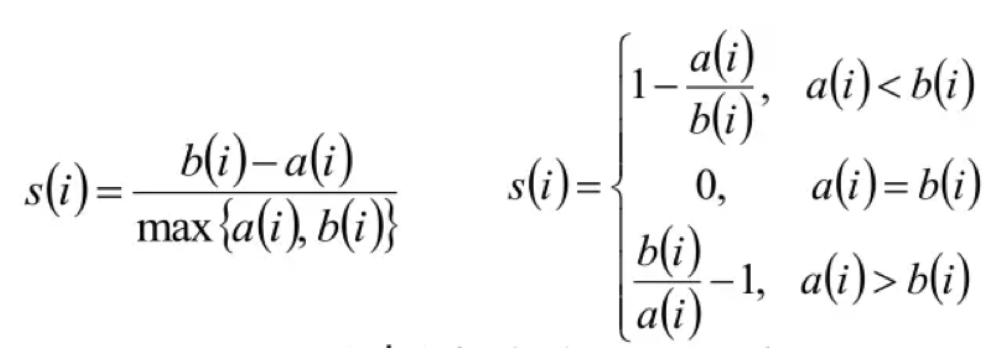
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。
平均轮廓系数的取值范围为[-1, 1],系数越大,聚类效果越好。
簇内样本的距离越近,簇间样本距离越远
[选读]CH 系数(Calinski-Harabasz Index)
类别内部数据的协方差越小越好,类别之间的协方差越大越好(换句话说:类别内部数据的距离平方和越小越好,类别之间的距离平方和越大越好),
这样的 Calinski-Harabasz 分数 s 会高,分数 s 高则聚类效果越好。
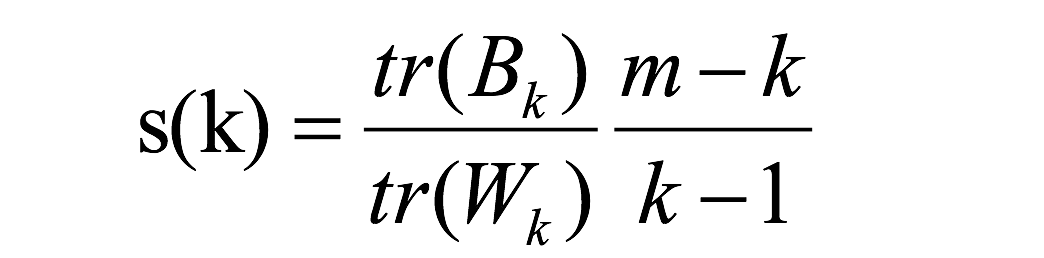
m 为训练集样本数,k 为类别数。
使用矩阵的迹进行求解的理解:
矩阵的对角线可以表示一个物体的相似性
在机器学习里,主要为了获取数据的特征值,那么就是说,在任何一个矩阵计算出来之后,都可以简单化,只要获取矩阵的迹,就可以表示这一块数据的最重要的特征了,这样就可以把很多无关紧要的数据删除掉,达到简化数据,提高处理速度。
CH 需要达到的目的:
用尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果。
