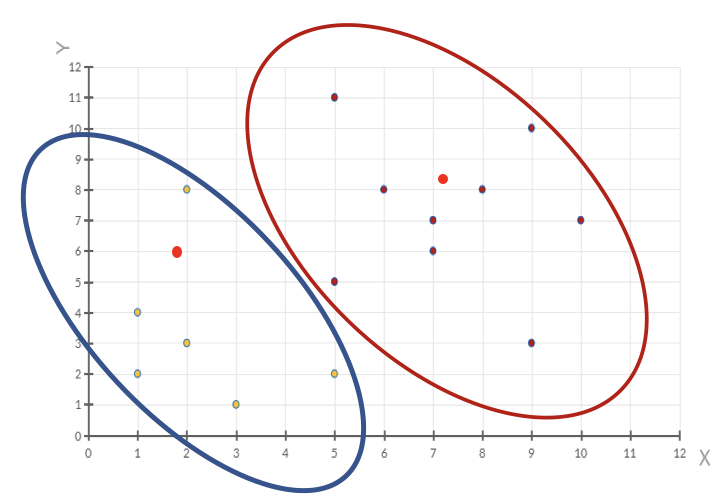
k-means 算法实现流程
K-means 算法是一种非常经典的无监督学习算法,它可以用来对数据集进行聚类。聚类是指将相似的数据点分到同一类,不同类的数据点尽量分开。
K-means 算法是一种无监督学习、聚类算法。
聚类步骤
- 随机设置 K 个特征空间内的点作为初始的聚类中心
- 对于其他每个点计算到 K 个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
- 接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
- 如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程
我们可以通过下图解释实现流程:
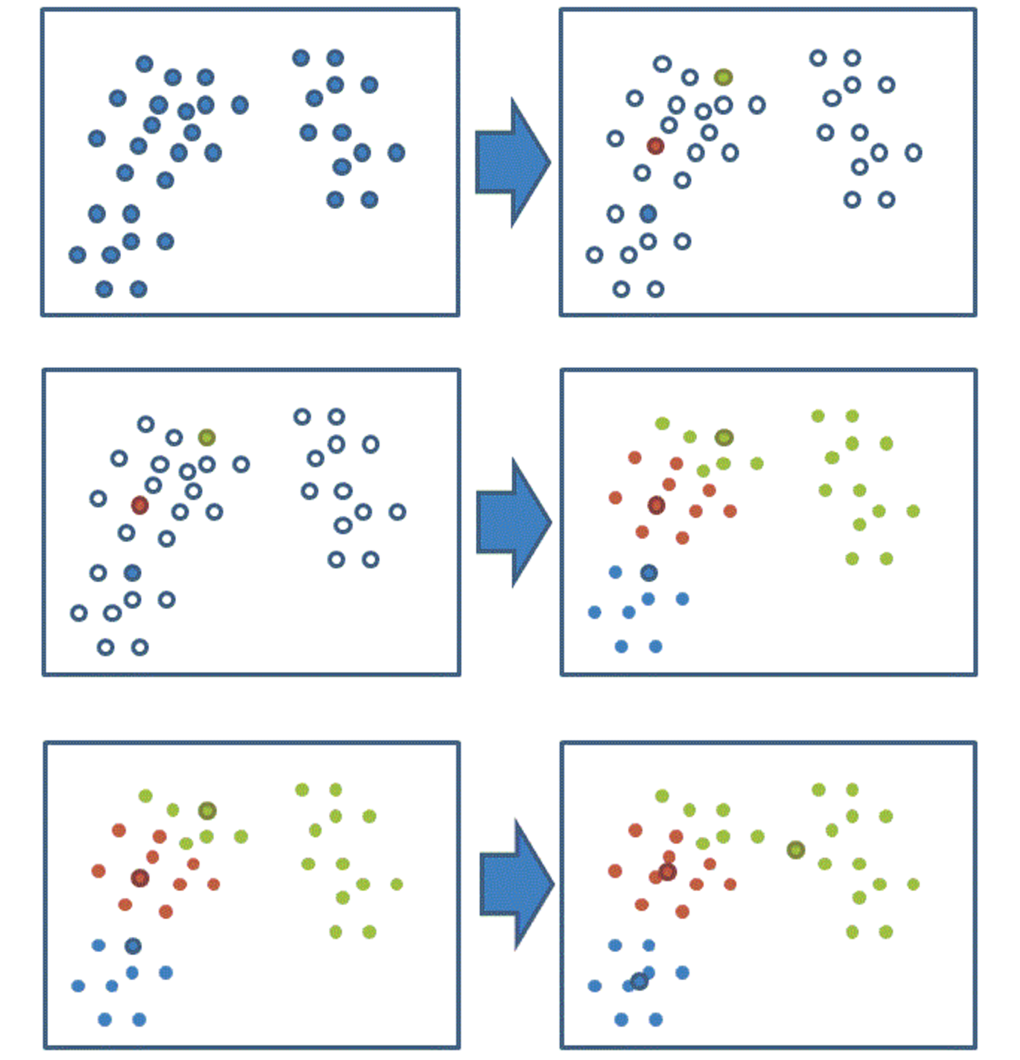
简单来说,就是将数据集分为 K 个簇,然后将数据集中的每个点分配到距离最近的 K 个簇中,然后重新计算 K 个簇的中心点,直到中心点不再移动为止。

从实现上就是这么简单。在原理方面,K-means 仍然利用了损失与优化的思想,即寻找使得损失函数最小的解。损失函数一般采用平方误差函数,即将每个点到其所属的簇的中心点的距离的平方和,我们将在后面的小节详细介绍。
由于第一步随机选取的位置不同,导致最终结果可能不同,我们实际上在实现 K-means 算法时,一般会多次随机初始化 K 个聚类中心,然后选择其中距离最小的作为初始聚类中心,然后迭代多次,选择结果最好的作为最终结果。
案例
下面我们模拟一个详细的聚类场景:
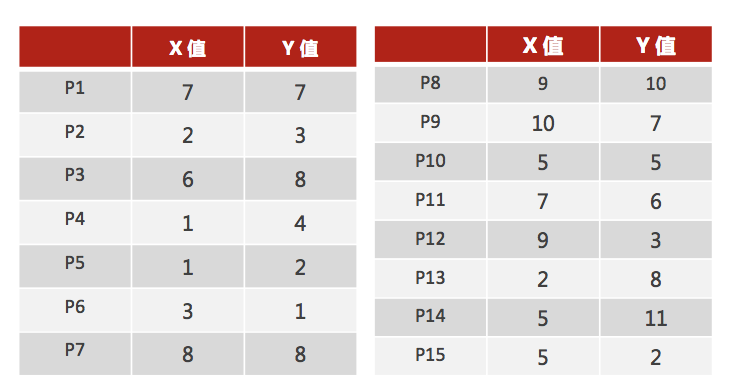
如图所示,我们有 15 组数据,每个数据包含 X 与 Y 值,我们希望这 15 组数据可以划分为 2 类,下面我们手动走一下 K-means 算法的步骤:
1.随机设置 2 个特征空间内的点作为初始的聚类中心(本案例中设置 p1 和 p2)
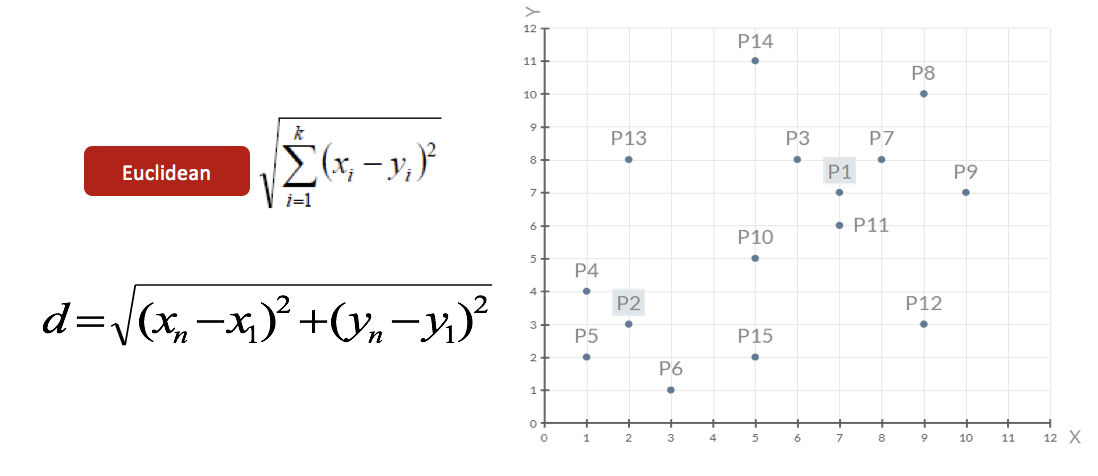
2.对于其他每个点计算到 K 个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
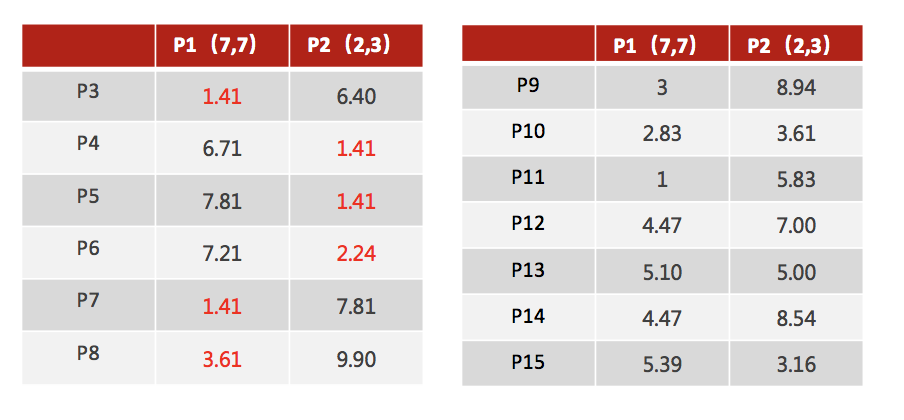
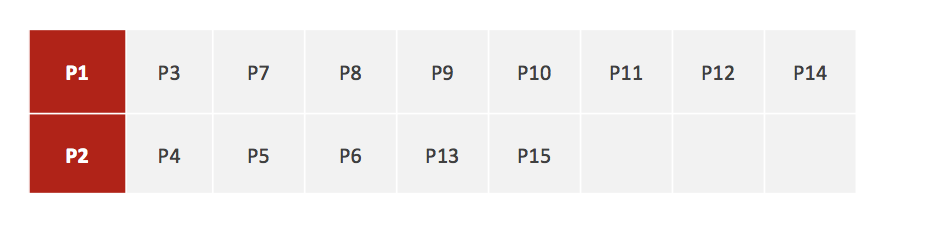
3.接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
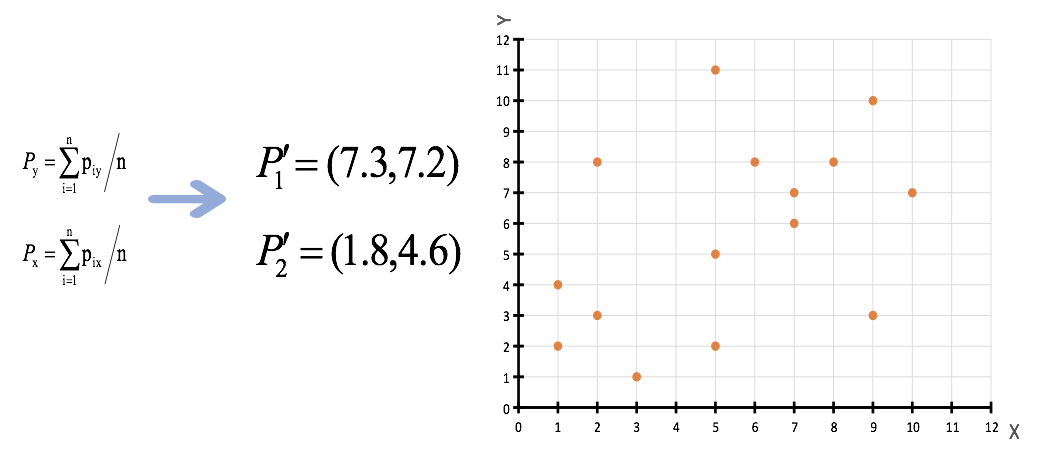
4.如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程【经过判断,需要重复上述步骤,开始新一轮迭代】
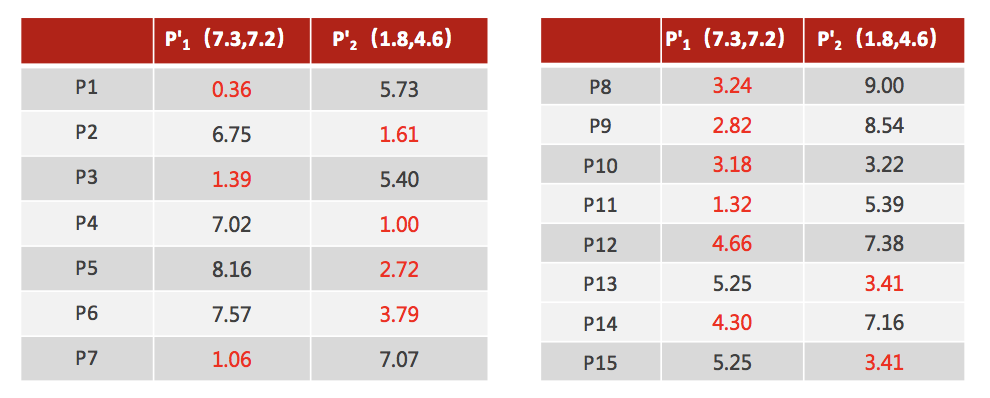

5.当每次迭代结果不变时,认为算法收敛,聚类完成,K-Means 一定会停下,不可能陷入一直选质心的过程。